運動学とは

---

 

まず運動学とは何だろうか？

 

力学をはじめとする様々な物理学の分野はそれぞれ「法則」や基礎となる「方程式」をもとにして構築されている理論である。

 

しかし、法則や方程式があるだけでは理論は構築できない。

 

それには物体の「運動」を記述する手段が必要である。

 

ここでは法則などはない状態で数学さえ知っていればできるような運動の記述について説明する。

 

その運動を数学的に記述する一般論こそが「運動学」である。

 

 

 

記述されるべき量

---

 

運動を数学的に記述しようにも何を記述するかを考えなければならない。

 

運動に関わる量には以下のようなものがある。

 

• 物体の位置
• 物体の速度
• 物体の加速度
• 時間

 

他にもあるかもしれないが、運動学ではこれらの量について分析していく。

 

 

 

一次元の運動

---

 

まずは一次元の運動を数学的に記述する。

 

 

位置

一次元の運動をする物体の位置は x とすれば良い

 

 

 

速度

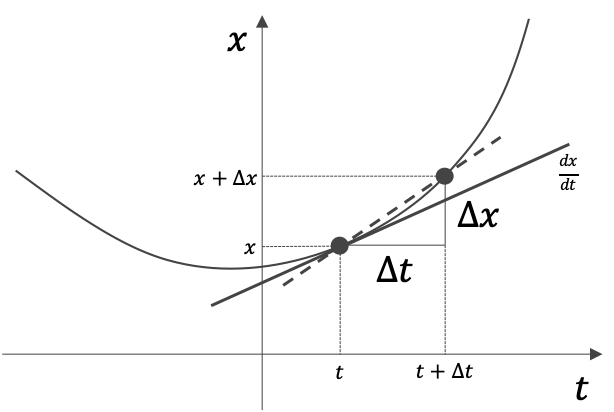
次に速度は位置 x と観測の間隔時間 Δt から以下のように求まる。

 

 

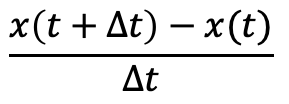
これは t から t+Δt あいだの平均速度である。

 

時刻 t における瞬間速度 v はΔt を限りなく小さくしていけば良い。

すなはち上の量を微分した量である。

 

 

 

 

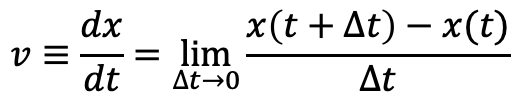
ちなみに時間に関する微分についてはドットを使った表記もあり、これはニュートンが考案した記法である。（詳しくはいずれ別途記事を書く）

 

 

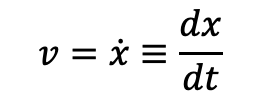
加速度

次に加速度は速度の時間変化である。

 

速度と同様、以下の量はt から t+Δt あいだの平均加速度をあらわす。

 

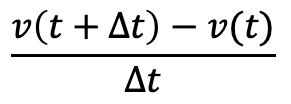
そして、時刻 t における瞬間加速度は Δt の極限をとった以下の式で表される。

 

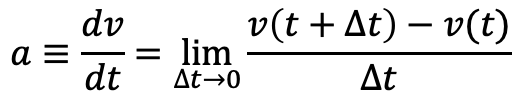
これは位置と以下のような関係にある。

 

 

 

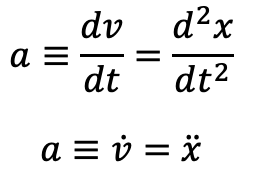
ここまでで一次元の運動について「位置」「速度」「加速度」の３つの表現が出揃った。

 

 

 

（応用１）等加速度運動

---

 

ここで１次元運動の応用例を考える。それが等加速度運動である。

 

16世紀にガリレオ・ガリレイが斜面に初速度0で球を転がす実験を行った。

その結果、移動距離が時間の2乗に比例することを発見した。このことから運動学的にどのようなことがわかるか考えてみる。

 

実験の結果は以下のような式で表される。

 

 

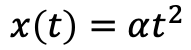
α は定数とする。

ここから速度と加速度は以下のようになる。

 

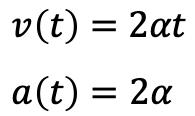
2α は定数であるからこの運動は加速度が時間によらない等加速度運動であることがわかる。

 

つまり、ガリレイが発見した「移動距離が時間の2乗に比例する運動」は「等加速度運動」だったということである。

 

ちなみにニュートン力学の視点で見れば、これは 2α=g sinθ (gは重力加速度、θは斜面の角度)としたものにほかならない。

 

 

 

一般的な１次元運動のモデル

---

 

ここで改めて1次元運動について具体的にイメージしながらモデル化していく

 

位置

まず、時間の経過ごとの位置の変化について、

Δt の時間経過の間に位置は速度 v(t) の分進む

 

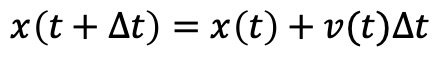
これは平均速度を v(t) として定義式を変形しても求められる。

 

ここでさらに時間をΔt 進めると、

 

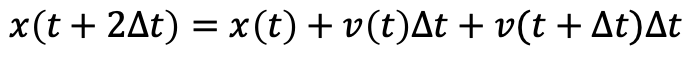
となる。

ここで基準の時刻 t を0として、時間をΔt 進める操作を n 回繰り返すと

 

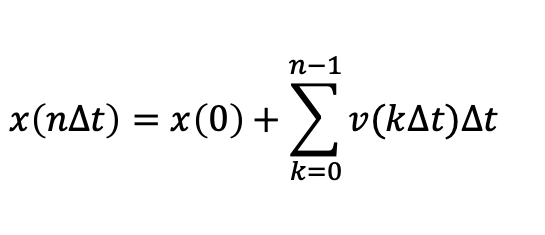
という式が得られる。

この右辺の第二項は区分求積法の式に他ならない。

 

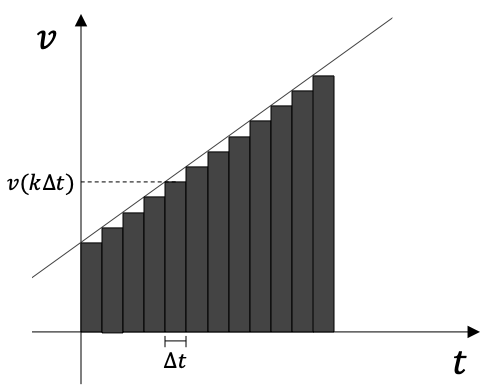
よって、ここから Δt → 0 、n → ∞ 、nΔt = t とすれば厳密な各時刻の位置が求められる。

 

これを式にすると以下のようになる。

 

 

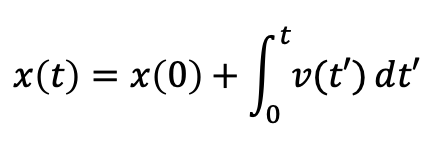
これはつまり、速度がわかっている状況であれば、初期位置 x(0) がわかれば位置の式 x(t) が決定できることを示している。

 

この式は以下のようにも求められ、速度 v が x の微分 dx/dt' であることとも合致している。

 

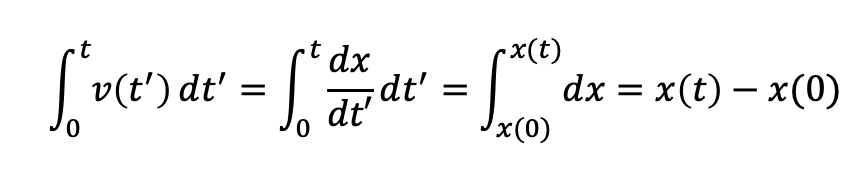
速度

位置と同様に速度も加速度を用いて積分で表現することができる。

 

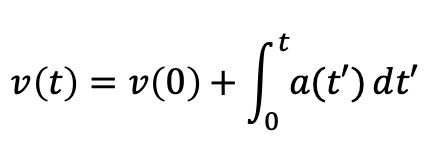
加速度も含めた位置

上の速度の式を位置の式に代入し、計算すると以下のようになる。

 

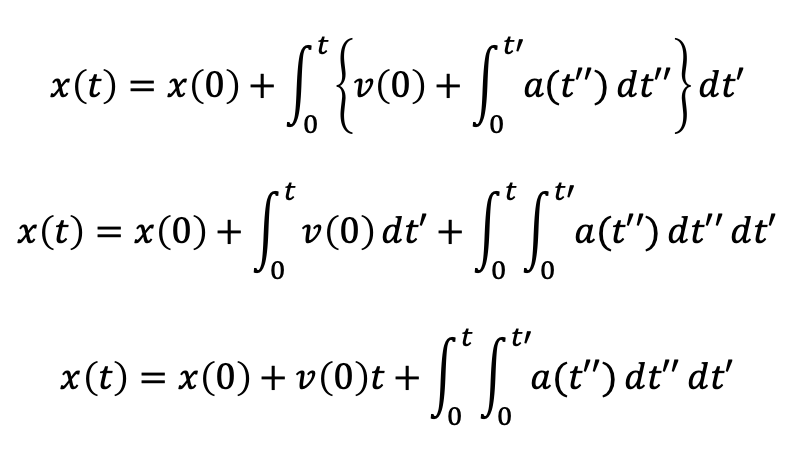
この3つめの式が加速度を使った位置の表現であり、加速度のみがわかっている状況で正確な位置の式を決定するには初期位置 x(0) と初期速度 v(0) の２つが必要であることがわかる。

 

速度がわかっている時は初期位置のみでよかった。

 

この辺りは微分方程式の理論が関連してくる。（その詳細は割愛する）

 

等加速度運動再び

上の式で加速度 a(t'') を定数 2α とし、初期位置、初期速度を0とすると（ガリレイの実験の設定）

 

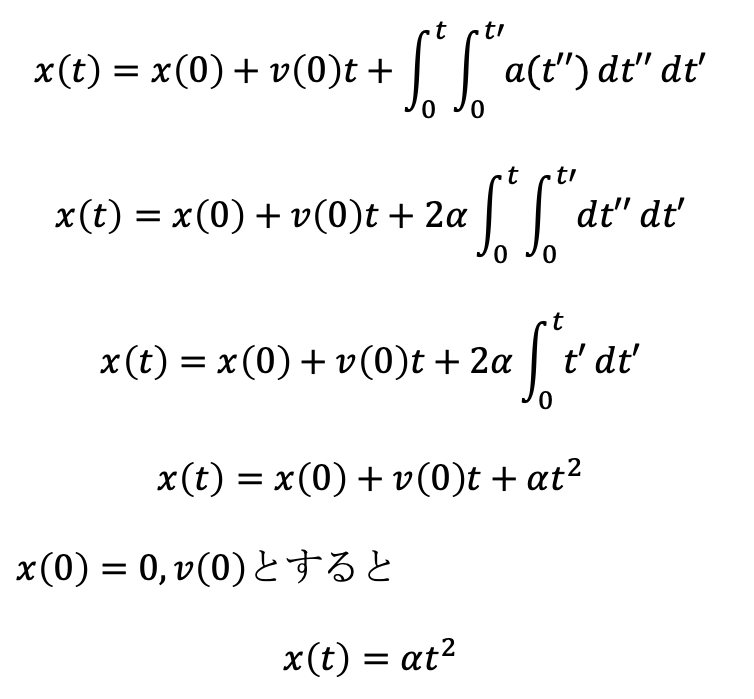
このように上のモデルはガリレイの実験を再現している。

 

 

 

運動学第１回まとめ

---

 

この回では物体の１次元運動を記述するために「位置」「速度」「加速度」の表現を説明し、ガリレイの等加速度運動の例を示した。

 

また、それぞれの量をつかって運動のモデル化した。それによってもガリレイの実験結果と合致していた。

 

今回の記事の中で重要そうなことを抜粋すると以下のようである。

 

• 速度は位置の微分、加速度は速度の微分である
• ガリレイの実験は等加速度運動の結果である
• 速度がわかっている時、位置の式を知るには初期位置が必要
• 加速度がわかっている時、位置の式を知るには初期位置、初期速度の２つが必要

 

また、モデル化の考え方は物理学だけでなく仕事でもつかえるものであり、いろんなことをモデル化する練習はしたほうがいいと筆者は思う。

 

次回は座標を導入し、2, 3次元運動を考える