ガリレオガリレイの基本情報
ガリレオ・ガリレイ
1564年〜1642年
イタリア
自然哲学者で天文学者、数学者。
近代科学的な手法の樹立に貢献をし、「近代科学の父」と呼ばれる。また天文学分野での貢献を称えて「天文学の父」とも呼ばれる。
業績
落体の法則
物体の落下の速さは物体の重さによらない
物体の落下による移動距離は時間の2乗に比例する
振り子の等時性
振り子の周期は振り子の振幅、重りの重さによらない
ガリレオ衛星の発見
木製の4つの衛星「カリスト」「ガニメデ」「エウロパ」「イオ」を発見
地動説への貢献
さまざまな実験、観測により地動説に有利な証拠を多数発見
これには「慣性の法則」も含まれる
筆者の印象
筆者のガリレオに対する印象について話したい。
これを話したくてこの記事を書いた。
筆者が小学生ぐらいの頃、ガリレオについては以下のように聞いていた。
- 実験によって、物の落ちる速さに重さは関係ないを発見した
- 実験によって、振り子の周期に振り子の振幅、重りの重さは関係ないことを発見した
- 観測によって、月のクレーターや木星の衛星を発見した
- 実験・観測結果から、地動説を支持
- 地動説を支持したせいで裁判で有罪になった
- 裁判で「それでも地球は回っている」と述べた
最後の２つは有名な話というだけだが、上４つの話を聞いて筆者は「実験とか観測でいろいろ見つけた人」という印象だった。
望遠鏡の製作や地動説の支持は歴史的な貢献ですごいと思っていたが、残りは確かにすごいけど実験とか観測ならガリレオじゃなくてもできただろうなと思い、有名さと凄さにギャップを感じていた。
しかし、この認識が間違っていたことを後で知った。
むしろそこには感動的な思考実験、洞察があったのだ。
この記事では、その感動したガリレオの思考を紹介する。
感動１ 落体の法則の思考実験
思考実験１ 物体の落下による移動距離は時間の2乗に比例する
最初に感動したのは落体の法則の「物体の落下による移動距離は時間の2乗に比例する」に関する発見についてである。
筆者が中学生くらいに読んでいた微分積分の本のコラムに上記法則の発見についてのガリレオの思考が書かれていた。
ガリレオはとりあえず落下時の移動距離と時間を測る実験をしたのかと思っていたが、実はそうではない。
彼はまず思考実験をして、その考えをもとに実験したのだ。
ガリレオは自身の著書「天文対話」の中で以下のように書いている。
どのような時間でもどれだけの時間でもよいから等しい時間を区切って、もし第１の時間に運動体が静止から出発してある距離たとえば一丈を通過したとすると、第２の時間には（そこから）三丈、第３の時間には（さらにそこから）五丈、第４の時間には七丈、このようにつづいてそれにつづく奇数に従うのです。つまり静止から出発する運動体の通過するそれぞれの距離は、それぞれの距離が通過されるのに要する時間の自乗の比率になる。言い換えると、通過される距離の比は時間の平方の比に等しいということと同じことです。
これは今の単位を使って現代風に要約すると以下のようになります。
運動体は1秒後には1m、2秒後には（そこから）3m、3秒後には（さらにそこから）5m ...と各時間間隔での移動時間が奇数になる。
これはつまり静止した状態から動いた運動体の移動距離は時間の２乗に比例するということだ。
最後の文章がどういうことかというと、
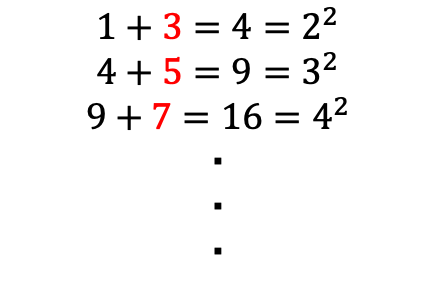というように、平方数に対応する奇数を足すと次の平方数になる。
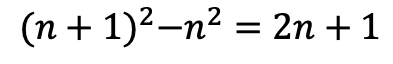
話がずれたが改めて、ガリレオは以下のようなことを考えたわけだが、どのようにこの考えに至ったのか。
運動体は1秒後には1m、2秒後には（そこから）3m、3秒後には（さらにそこから）5m ...と各時間間隔での移動時間が奇数になる。
これはつまり静止した状態から動いた運動体の移動距離は時間の２乗に比例するということだ。
天文対話には以下のような図がある。（実際のものではないがそれをわかりやすくしたもの）
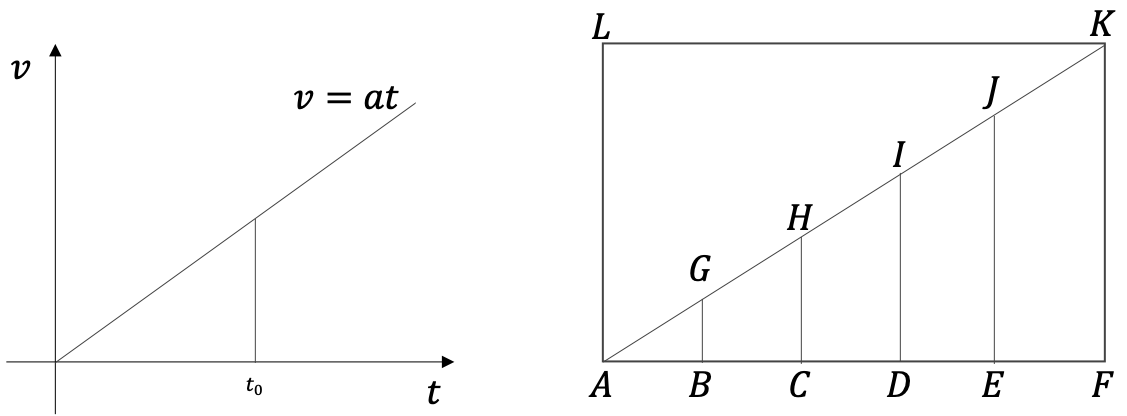
左図の横軸は時間、縦軸は速さを表す。右図ではAB,BC...が等しい時間間隔を表す。
運動体がAから動き始めて、時間ABだけ経過すると、速さがBGになる。さらに同じ時間BCが経過すると速さはCHになる。
つまり、速さが一定の割合で増える。
そのときの移動距離についてガリレオは以下のように考えた。（天文対話の文を少し変えたもの）
時間ABの間に速さがBGになるのに先立って、線AB上にある無限の点に対応した、時間AB上にある無限の瞬間に得られる無限の小さな距離が通過されることは明らかです。..... この線の無限性は結局、三角形AGBの面積で表されます。
つまり、ガリレオは運動体が静止状態から出発して一定の加速運動をして通過する（時間ABの間の）移動距離は三角形AHDの面積で表されると主張している。
同様に、時間BCのあいだの移動距離は台形BGHCの面積である。
ここで三角形AGBの面積を1とすると、台形BGHCの面積は3、台形CHIDの面積は5である。（相似の関係を使えば簡単に計算できる）
ここからガリレオは最初の考え「移動距離は1, 3, 5, 7...と増えていく」と考えたのである。
少し複雑になったが、簡単にいうと、ガリレオは独自に微分積分の考えを用いて落下運動を考察し、仮説をたて、実験によって自分の考えを証明したのである。
ちなみに微分積分を発見した１人ニュートンはガリレオが亡くなった年に生まれた。
ガリレオは次の時代に発見される数学に近い考えをすでに展開していたのである。
思考実験２ 重さの違う２つの球を繋ぐ
そして、調べてみると「物体の落下の速さは物体の重さによらない」についてもガリレオは思考実験を考えていたことがわかった。
ガリレオ以前にアリストテレスが「重いものはより速く、軽いものはより遅く落下する」と主張しており、正しいと信じられていた。
これについて、ガリレオは思考実験と実際の実験で否定した。
以下のような実験を考える。
- 重い球と軽い球を用意する
- ２つの球を細い糸で繋ぐ
- 同時に落下させる
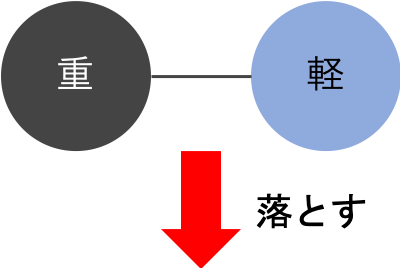
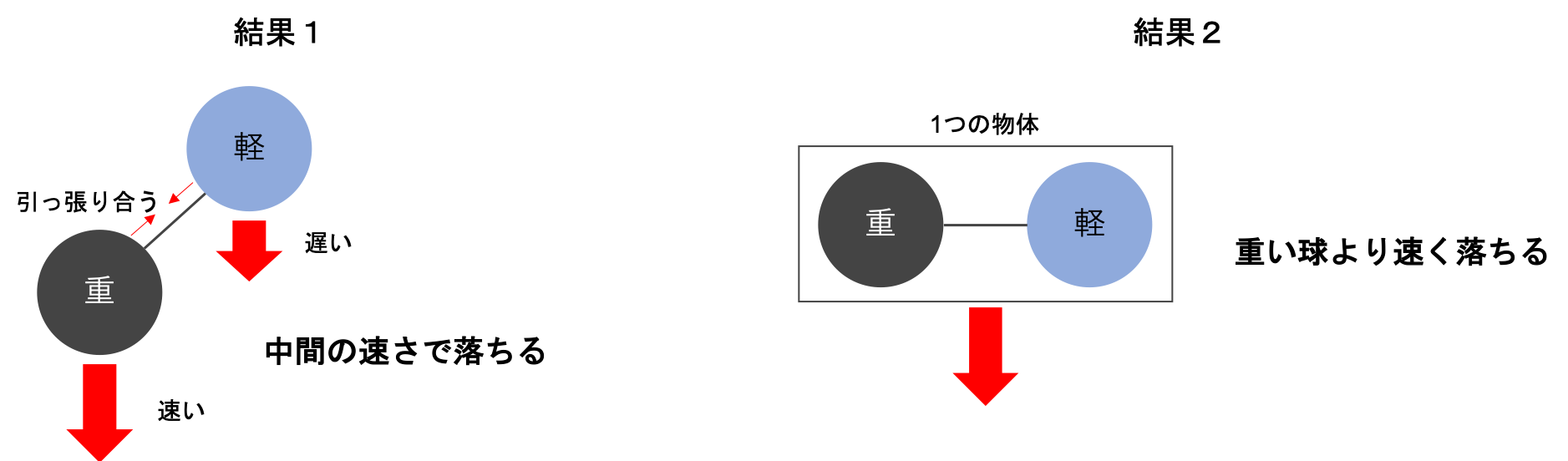
アリストテレスが正しいとすると、この思考実験の結果は２つの結果が考えられる。
結果１
重い球は軽い球に引っ張られ、細い球は重い球に引っ張られるので中間の速さで落ちる
結果２
２つの球は繋がっており、１つの物体と考えられるので重い球単体よりも速く落ちる
このように矛盾する２つの結果が出るのはおかしいので、アリストテレスの考えは間違っていると思われる。
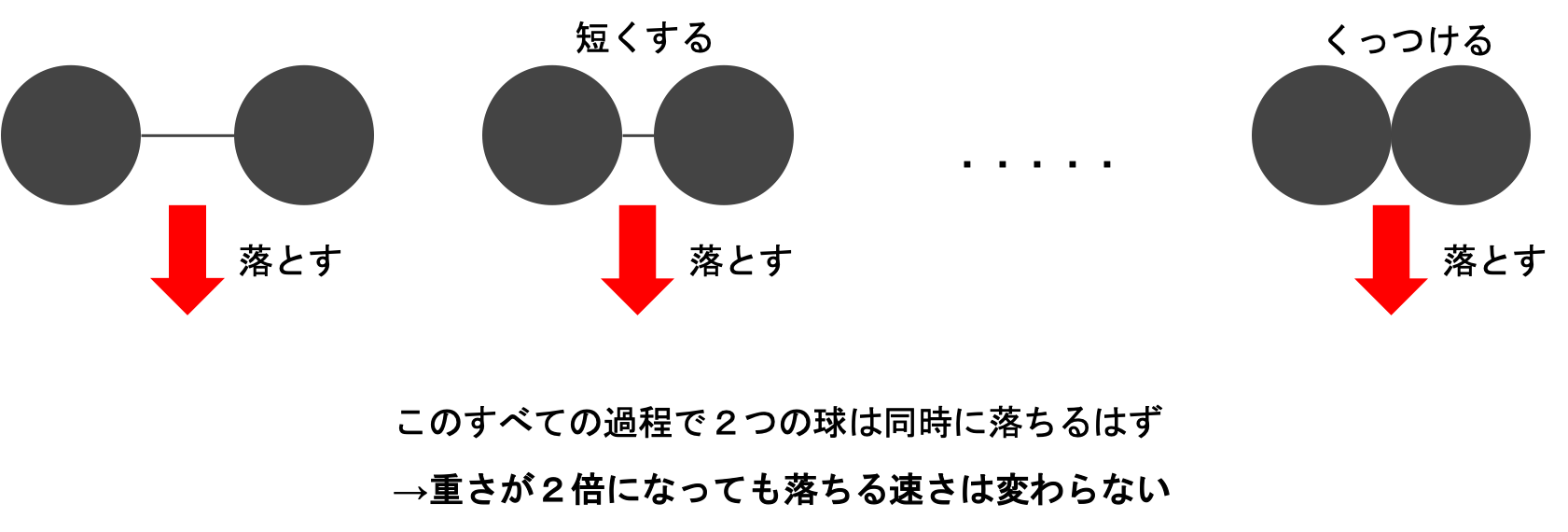
思考実験３ 同じ重さの球を繋ぐ
- 同じ重さの球を２つ用意する
- ２つの球を十分に細くて軽い糸で繋ぐ
- 同時に落下させる
- 糸を短くしていき最後、球をくっつけて落下させる
この実験はこのようになると考えられる。
十分に細くて軽いので２つの球は単体で落とす時と同じ速さで落ちる
２つの球は同じ重さなので同時に落ちる
糸を短くしていき、くっついてしまうと２つの球は１つの物体と考えられ、２倍の重さになるが糸が長い時の延長の結果のはずなので単体の時と同じ速さで落ちる
これはつまり、重さが2倍3倍・・・となっても落下する速さは変わらないことを示している
これらの思考実験からガリレオは落下の速さが重さによらないと考え、その後実験で確かめたのである。
感動２ 慣性の法則の思考実験
地動説を有利にした１つの証拠に「慣性の法則」がある。
ガリレオは実はこの法則も思考実験と実際の実験によって示したのである。
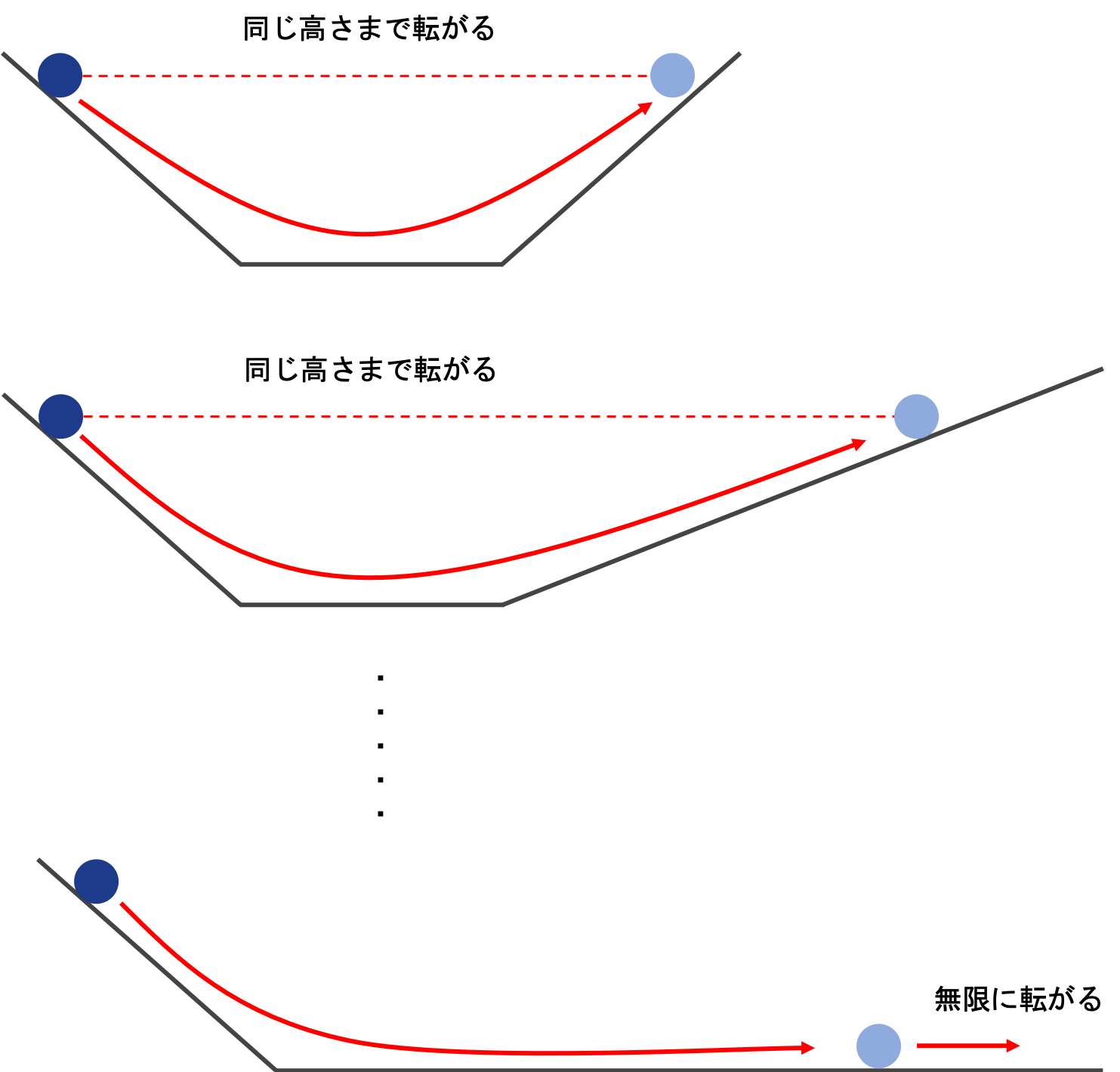
思考実験４ 慣性の法則
- U字型のレール上で球を転がす
- 球の初期位置と反対側を低くしていく
- 球の初期位置の反対側を平らにする
この結果はこうなるはずだ。
まず１の結果として、転がる球は初期位置と反対側の同じ高さの点まで転がり戻っていく。
そのレールの坂が緩やかになれば球の転がる距離が長くなる。
レールが平らになったらそのまま無限に転がっていくはずだ。
これが「慣性の法則」である。（厳密には少し違う）
このようにガリレオはただ実験するのではなく、思考実験によって深い洞察を得て実際の実験で正しさを示しているのである。
筆者はこのようにしっかりと思考をしている人（ガリレオはしっかりとなんてレベルではないが）が大好きである。
最初ガリレオのことはただの実験、観測の人と舐めていたが、よく知れば大好きなタイプの科学者で今では謝罪の気持ちもありつつ、推し科学者の１人である。
（ちなみに筆者は今では実験家の洞察などにも凄さを感じているので実験家、観測家の人も決して舐めていない）
まとめ
今回は有名科学者ガリレオ・ガリレイについて書いてみた。
ガリレオは数々の業績を残し、そこには実際の実験だけではなく、適切な思考実験や結果に対する考察など深い洞察と思考が伴っている人物である。
紹介した思考実験以外の業績でもしっかりとした考察がある。
また、その思考の中で未来で発見されるようなこと（微積分や慣性の法則）を先んじて洞察を得ていた。
筆者はガリレオの思考はとても美しいと感じた。
ガリレオだけではないが、適切な思考実験で深い論理展開ができる人の思考は美しくて魅力的だと思う。
筆者のガリレオに対する評価も爆上がりして、今では推し科学者の１人となっている。
みなさんもぜひガリレオ・ガリレイを好きになってほしい。また、推し科学者を探してみてはいかが？
＼ よかったらシェアしてください！ ／
![第１回[運動学]1次元運動のサムネイル](https://fumilabo.com/thumbnails/17038419781次元運動.png)
