成功した計算方法

---

前回の計算と実験で正三角形を正方形に見ることができた。

 

その時の計算方法はおおよそ以下のようであった。

 

1. 正三角形をxy平面上に適切に配置する
2. 視点を配置する
3. 正三角形を傾ける
4. 視点からの各点への視線と平面の交わりを求め、正方形の配置になるように計算する
5. 傾いた正三角形から高さの線を伸ばし、視点と正方形のもう１つの点を繋いだ視線との交わりを求める

 

 

これにより必要なパラメータ（視点との距離、傾ける角度、錐の高さ）が求められた。

 

今回はこれを一般化し、n→n+1が可能かどうか、できるとしたらその方法（パラメータ）を求めていく

 

 

 

一般化した計算…の前に

---

 

上の方法をそのままnに置き換えれば…

 

と言いたいところだが、そう簡単にはいかない。

 

 

一般化する上で考えるべき点がある。

 

まず、一般的な正n角形の座標上での表現方法である。

 

これは複素数の考え方を応用すれば一瞬でわかる。

 

z^n = 1の解が正n角形の配置になるというのは知っている人も多いのではないだろうか（数Ⅲ？かなにかでやったような気がする）

 

この計算はド・モアブルの定理を使って以下のように計算し、頂点の座標を導ける

 

 

 

また、正n角形は2πをn等分しているという考え方でも上記の式を導ける。

 

 

もう１つ考えるべき点として、手順1の「適切な配置」についてである。

 

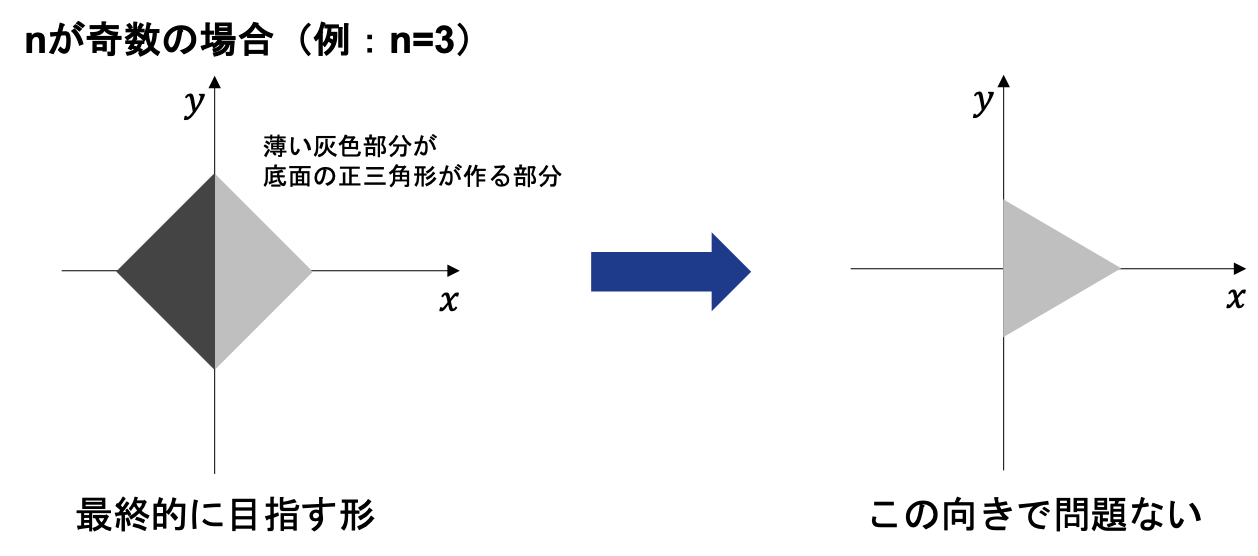
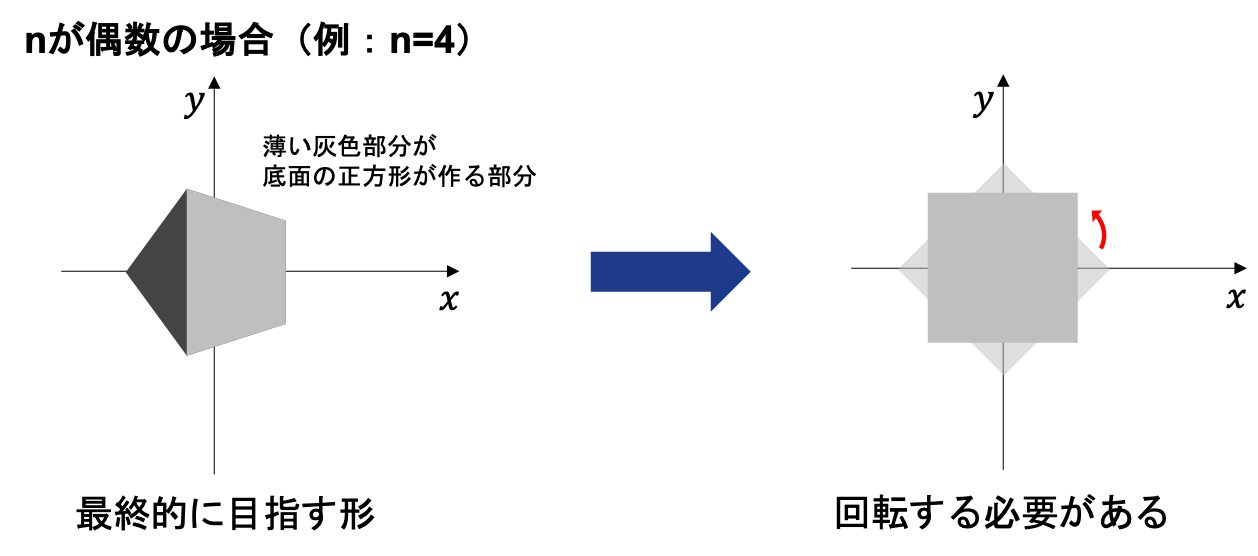
nが偶数か奇数かということだ。

 

上の表式はm=0の点が必ずx軸上の点に存在する配置だが、最終的に錐の頂点がx軸上に来るため、nが偶数のときは少し回転する必要がある。

 

 

また、配置についてもう１つ考えなければならないことがある。

 

原点の位置である。

 

上の表式で求めた点の配置は正多角形の重心を原点に置いた配置である。

 

だが、傾ける前にこの点をずらさなければいけない。

 

例えば正三角形の場合は１つの辺の中点が原点になるようにずらさなければならない。

 

 

 

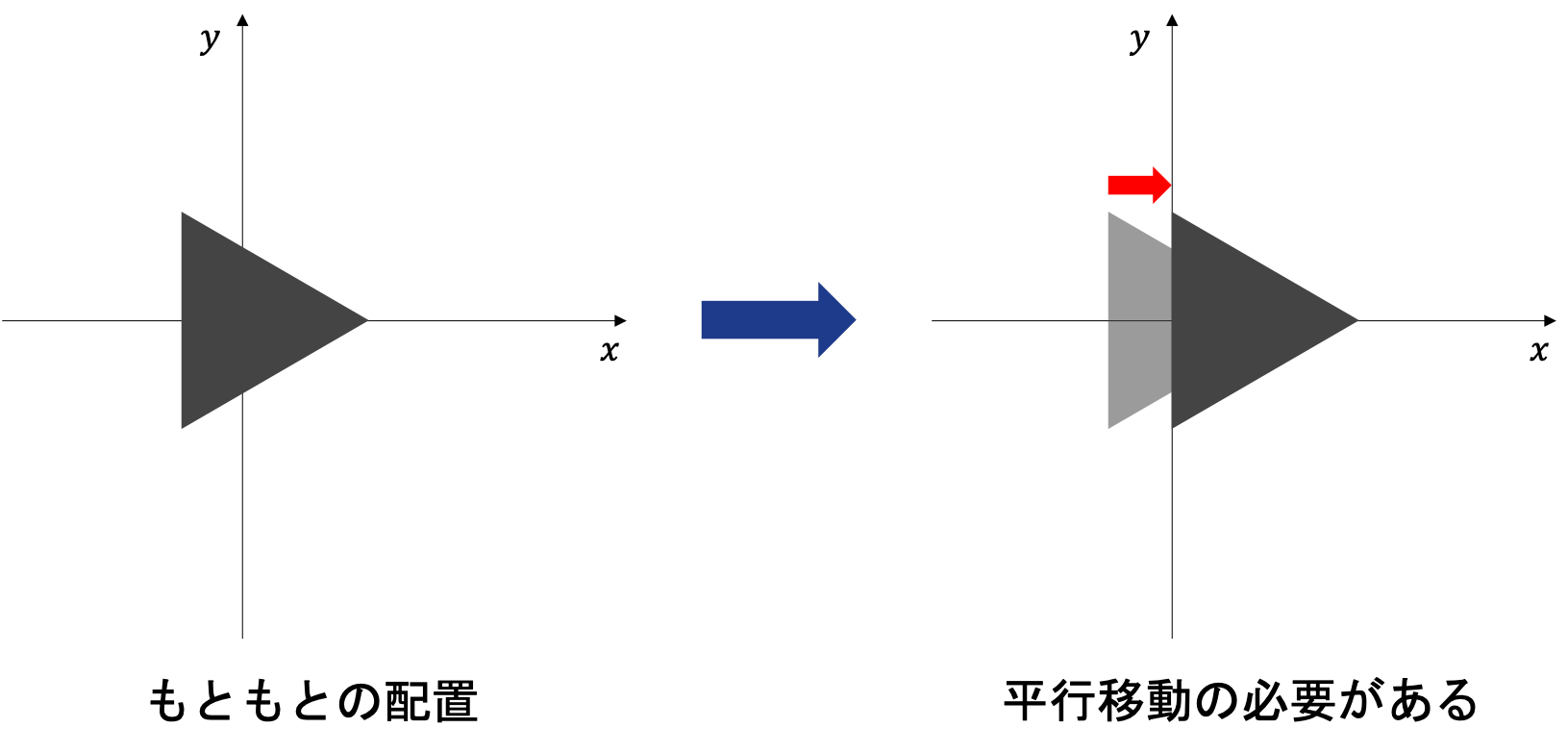
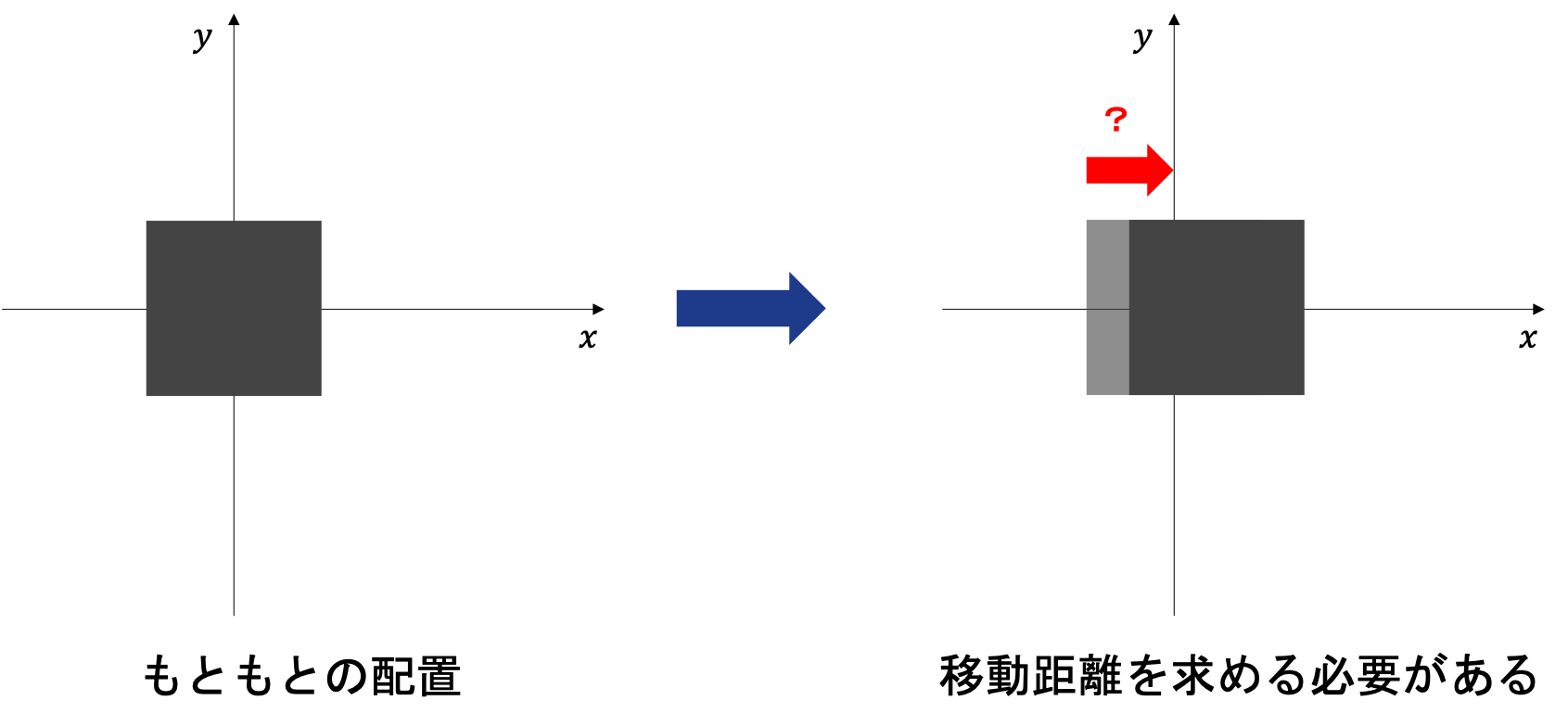
正三角形から正方形の場合は三角形の1辺の中点が正方形の中心になることが自明だが、一般的には自明ではない。

 

よって、一般化するに当たって、前回とは違ってもう1つパラメータが増える。

 

つまり、上の表式でもとめた各点を、傾ける前に平行移動させる操作があり、どれくらいずらすかを求める必要がある。

 

 

 

 

 

一般化した計算

---

 

ここまでを踏まえて計算手順を一般化すると以下のようになる

 

1. nの偶奇を含め、一般化しされた正n角形の点の表式を求める
2. 図形をx方向に並行移動する
3. 視点を配置する
4. 図形をy軸を中心に回転させる
5. 視点からの各点への視線と平面の交わりを求め、正n+1角形の配置になるように計算する（1の偶奇による回転を考慮する必要がある）
6. 傾いた正n角形から高さの線を伸ばし、視点と正n+1角形のもう１つの点を繋いだ視線との交わりを求める

 

ということで、ここから詳しく計算していく。

 

1. nの偶奇を含め、一般化しされた正n角形の点の表式を求める

 

まず、正n角形の点の表式は以下である。

 

 

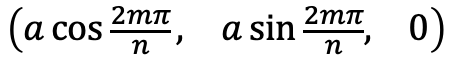
手順5でも必要になるのでこの点を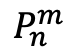とおく

 

ただし、これはnの偶奇を考慮していない。

 

偶奇を考慮すると、nが偶数の時だけ点の座標をπ/nだけ回転させる必要がある。

 

 

 

 

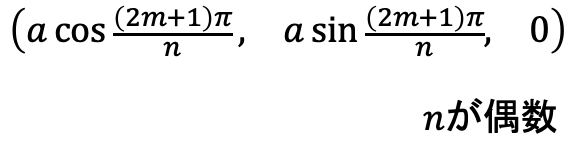
よって、この回転を偶数の時だけプラスするので奇数は0、偶数は1となるような式があると都合がいい。

 

そのような関数をそのまま定義してもいいが以下の式がそれを満たしている。

 

 

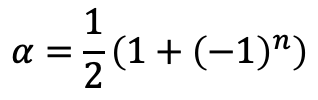
これをαとおく。

 

これを使うと、nの偶奇も考慮した正n角形の点の表式は以下のようになる。

 

 

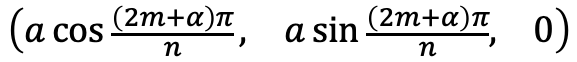
これでxy平面上に正n角形が配置された。

 

 

 

2. 図形をx方向に並行移動する

 

次に、回転する前の平行移動操作である。

 

これは最終的に出来上がる正n+1角形の重心が原点に来るようにする操作である。

 

この操作は簡単で各点のx座標の値に+Lすれば良い。

 

 

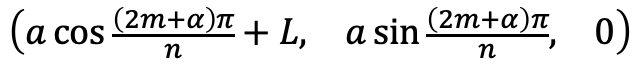
これで図形を回転させる前準備が整った。

 

 

 

3. 図形をy軸を中心に回転させる

 

これは正三角形の時と同様に、回転行列をかけた座標を求めればよい。

 

使う回転行列はy軸中心に右ネジの回転方向に回転させる回転行列であるから

 

 

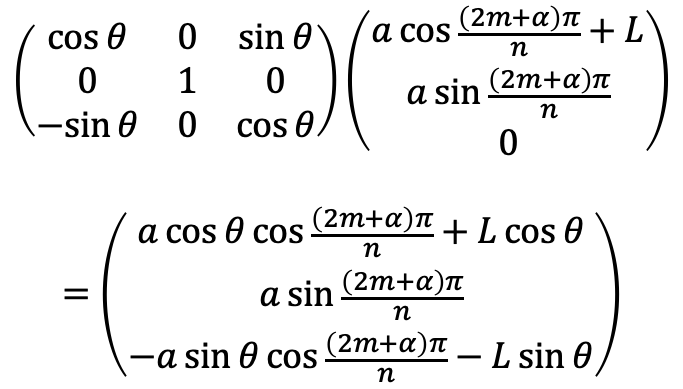
ここまでで求めた各点の座標を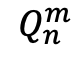とおく。

 

 

 

4. 視点を配置する

 

これも正三角形のときと同様にz軸上z=Hの点を視点とする。

 

 

 

 

5. 視点からの各点への視線と平面の交わりを求め、正n+1角形の配置になるように計算する（1の偶奇による回転を考慮する必要がある）

 

まず、正三角形の時と同様に視線とxy平面の交わる点を求めていく。

 

 

 

次にnが偶数の場合は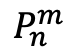での点の配置（x軸正の位置にm=0の頂点がある配置）に合わせてこの点を回転させる必要がある。

 

 

 

nが奇数の場合、π回転させてもさせなくても同じであるから、nによらず回転した方が計算しやすい。

 

よって、以下の式となる。（zは反転させないが、0なので-を前につけている）

 

 

 

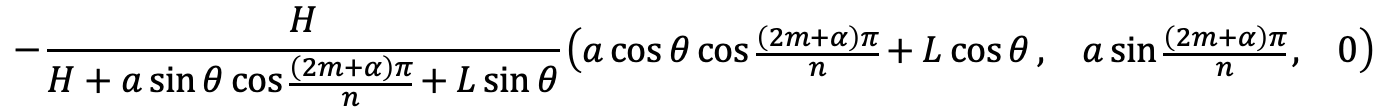
この求めた点をとする。

 

次に、この求めた点が正n+1角形のどの点と対応するかを考えると、以下のようになっているので

 

 

 

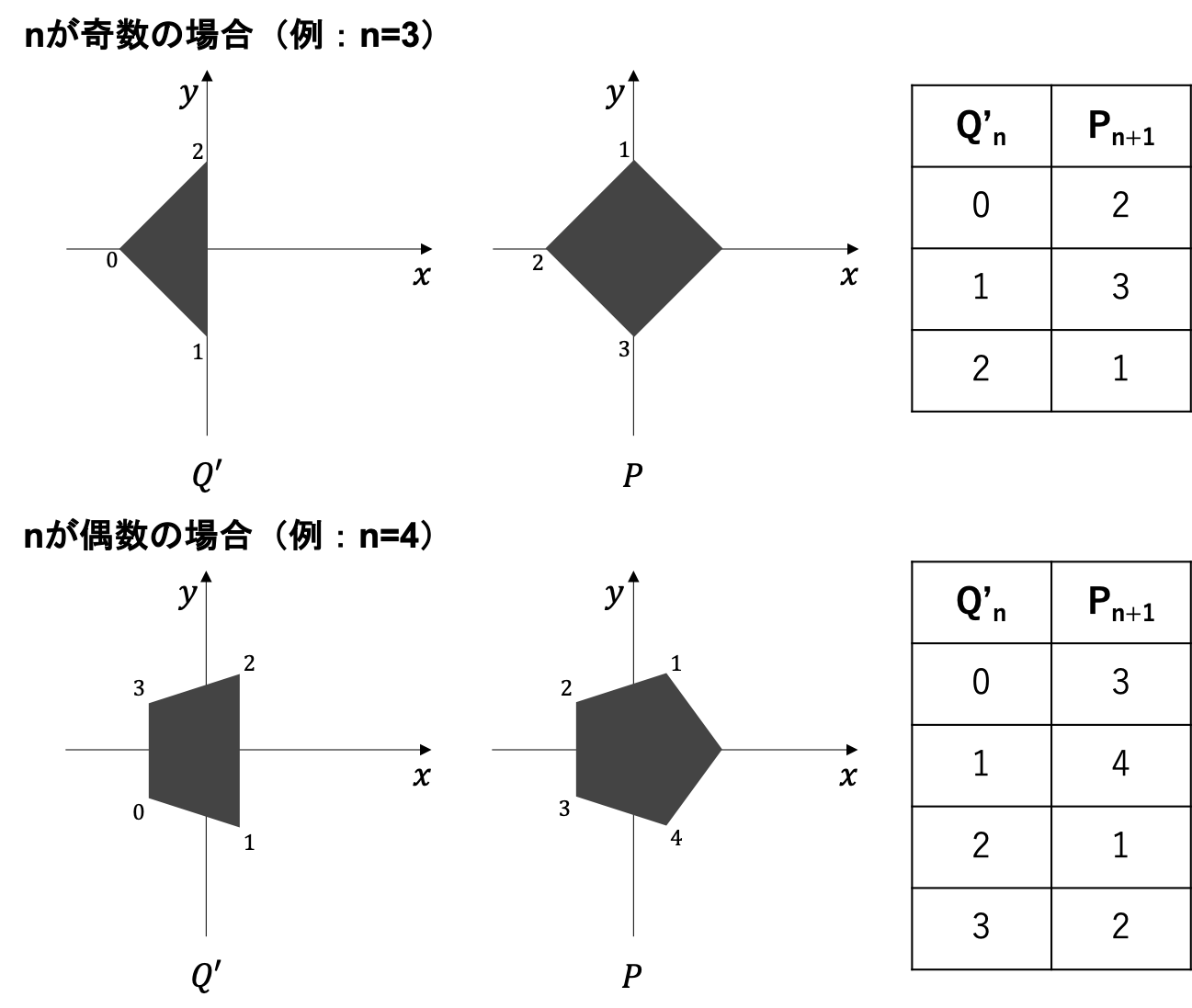
これを一般的に考えると、

 

nが奇数の場合、まず正n角形のm=0が正n+1角形のm=(n+1)/2に対応し、正n角形のm=(n-1)/2までは正n+1角形でも１ずつ増えていく。それ以上ではパターンが変わるが、座標を対応させる上で、対称性を持っているのでここまでのmの範囲で十分である。

 

nが偶数の場合、まず正n角形のm=0が正n+1角形のm=(n+2)/2に対応し、正n角形のm=n/2-1までは正n+1角形でも１ずつ増えていく。奇数と同様それ以上は無視していい。

よって、以下な式が成り立てば正n角形の点が正n+1角形のn個の点に一致することがわかる。

 

 

 

 

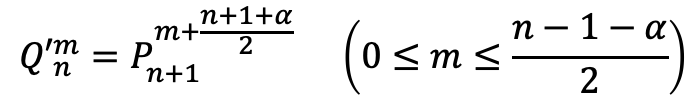
求めた式からわかること

---

 

さて、本当なら上の対応を方程式として解いてパラメータを定めればいいのだが、その前に画像からわかることを考察してみよう。

 

まず、このの点の配置が正多角形の配置になっているなら原点からの距離がすべて等しくなっているはずである。

 

 

すなわち、この各点の原点からの距離がmによらないということである。

 

ということで、原点からQ'の点までの距離を求めてみると以下のような式になる。

 

 

 

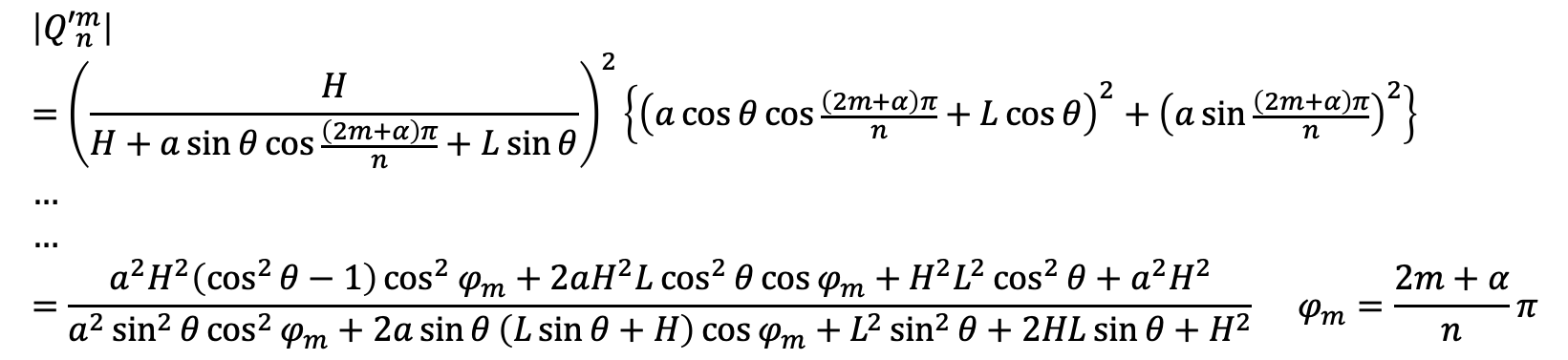
これが定数とおくと以下のようになる。

 

 

 

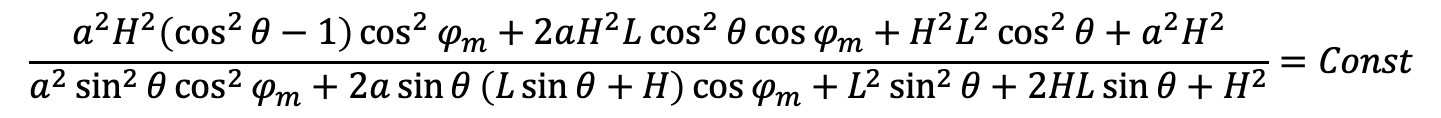
これをよく見てみると、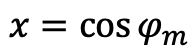のように置いて、係数を適当に文字に置換すると以下のように表せることがわかる。

 

 

 

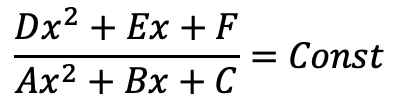
これは2次方程式になっている。

 

つまり、この方程式は２つしか解をもたない！

 

これは何を意味しているだろうか？

 

この方程式はもともと「mを変数とする」方程式であった。

 

そして、この方程式は最大2つしか解をもつことができない。

 

ということはmが3つ以上ある場合はこの方程式を成り立たせることができないのである。

 

mの範囲は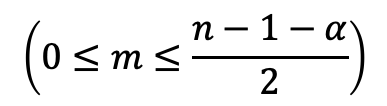

であるから、mが3つ以上ある場合（m=0,1,2）とはnが5以上の場合である。

 

 

 

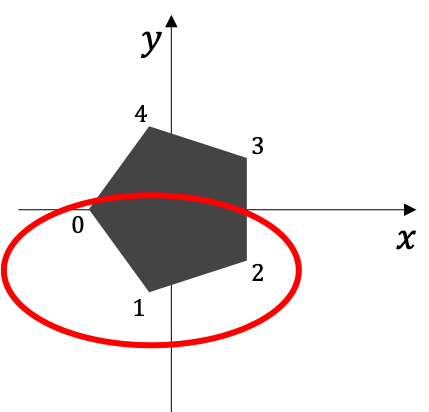
よって、n≧5では正n角錐を正n+1角形と見ることができない！

 

 

 

問いの答え１

---

 

ここでもともとの問いに1つの答えを得ることができた。

 

遠近法を考慮することで正四角錐から正五角形を作ることは可能か。

また、一般的に正n角錐から正n+1角形を作ることは可能か。可能であるとすればどのようにすれば良いか

 

この「一般的に正n角錐から正n+1角形を作ることは可能か」の問いの答えは「n≧5では不可能」である。

 

n≦2では適切に正n角形を定義すればできるような気がする。

 

 

 

今回のまとめ

---

 

今回の考察で問いの一部に答えを得ることができた。

 

元々の問いは以下であった。

 

遠近法を考慮することで正四角錐から正五角形を作ることは可能か。

また、一般的に正n角錐から正n+1角形を作ることは可能か。可能であるとすればどのようにすれば良いか

 

この「一般的に正n角錐から正n+1角形を作ることは可能か」に対する答えは「n≧5では不可能」である。

 

私はこの答えが得られた時、とても残念に思った。

 

だが、最後にとりあえず正四角形から正五角形を作る計算と実験はしようと思った。

 

次回、その計算とそこでわかった驚くべき事実を紹介する。