前回

遠近法による見かけ上の大きさの計算方法を考えたが、単純な距離に比によって見かけ上大きさを計算する方法はうまくいかないことに気づきました。

今回は見かけの形、大きさの正しい計算方法に関する考察についてお話しします。

遠近法に関する考察

あらためて対象がどのように見えるかについて考察してみました。

正しい計算方法に気づいたのは、ある日高いビルを見上げていたときでした。

ビルを見上げると当然ですが以下のようになっていました。

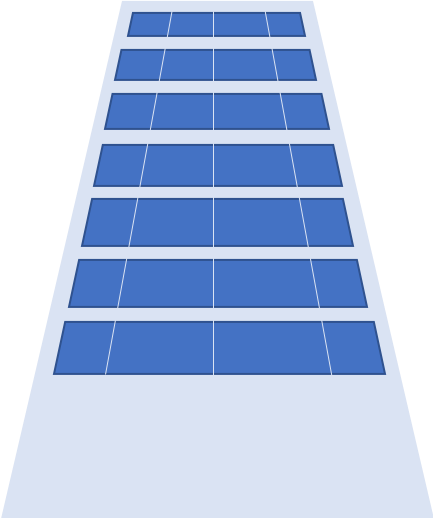
ビルの幅が上に向かって狭くなっています。

ビルの幅は平行で変わらないはずですからまさに遠近法です。

ここで私はあることに気が付きました。

対象との距離の変化で対象を収める角度が変化する

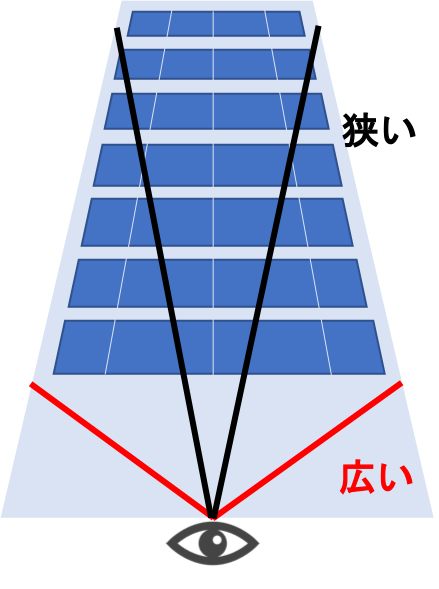
このことから以下のように考察しました。

対象の端（境界）の点と視点とを結んだ角度が同じであれば対象がどの距離にあっても同じ大きさに見える

下の図のような感じです。

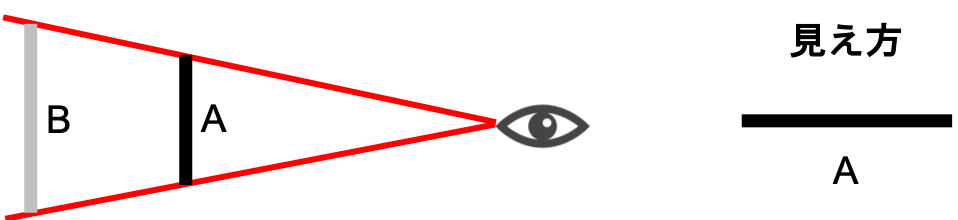
この場合Aの棒とBの棒の端と視点を結んだ角度が同じなので、AとBの距離は違いますが同じ大きさに見え視点からはAにちょうどBが重なって見えるでしょう。

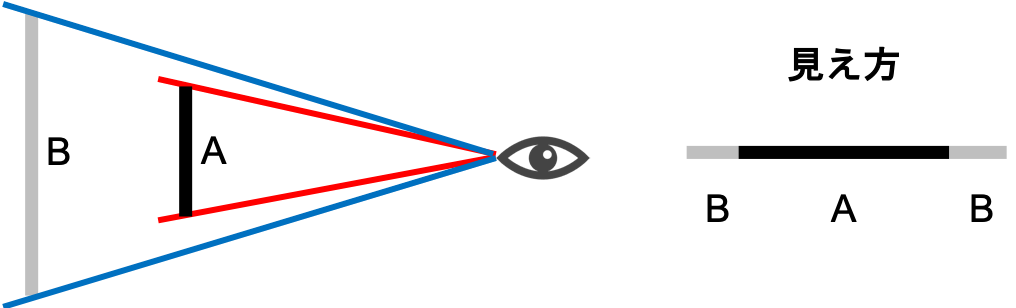
一方でこの図では、Aの端と視点を結んだ角度よりBの端と視点を結んだ角度が大きいのでBがAより大きく見えるでしょう。

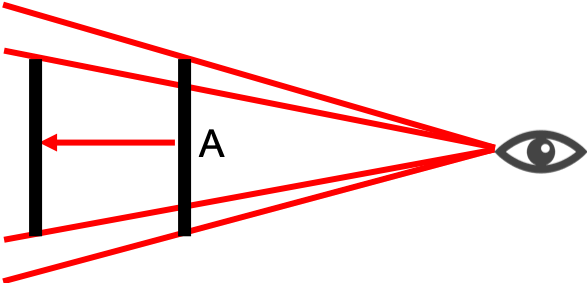
対象が遠ざかるとそのぶん端と視点を結ぶ角度が小さくなるので対象の大きさも小さくなるということです。

これが遠近法の正体であると考えました。

計算方法の検討

ここで計算方法を再検討してみました。

上記の遠近法の仕組みに加えて、２つ以上の対象がある時にその全体の見え方がどのように決まるかについて考えてみました。

全体が下図のようになっていたとします。

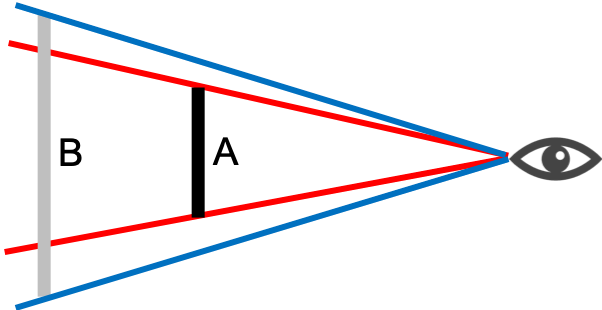
ここで視点の前の任意の箇所に平面を設置します。

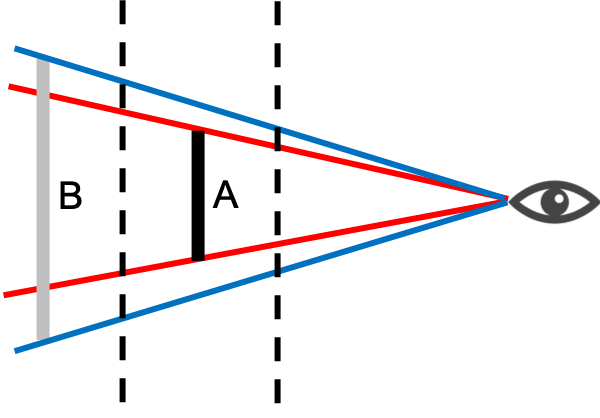
このとき、相似の計算から、平面をどこに設置しても青の視角の幅と赤の視角の幅の比は変わりません。

つまり設置した平面には「見え方」である以下のような図が射影され、大きさは平面の設置箇所によりますが、「形状」は設置箇所によりません。

よって、以下のような考察ができます。

対象の見かけの形状は「対象の各点と視点を結んだ直線」と「視点の正面にある平面」との交点によって決まる

すなわち、以下のような計算をすれば良いことになります。

（複雑になりそうだったのでまず正三角形から正方形を作ります）

1. 正三角形を以下のように設定する

2. z軸上に視点を設定する

3. 三角形をy軸を中心に時計回りにθ回転する

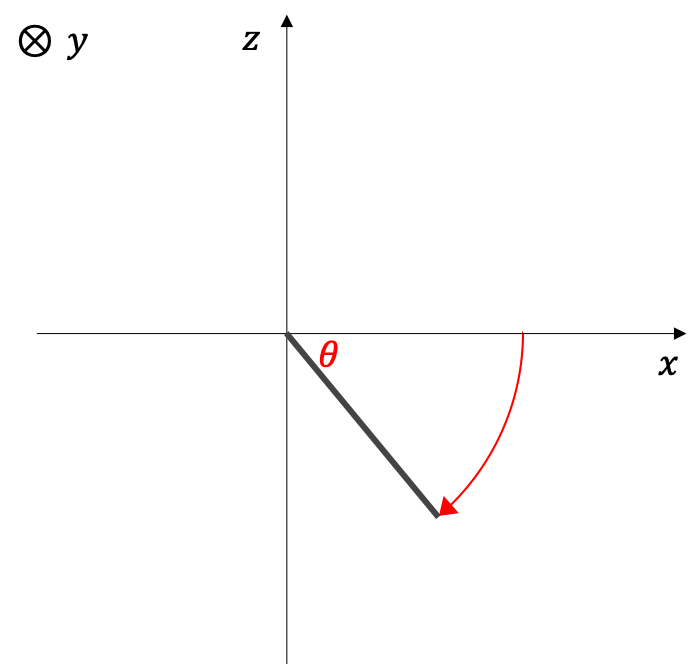
4. 視点と三角形の各点を繋いでxy平面との交わる点の式を求める

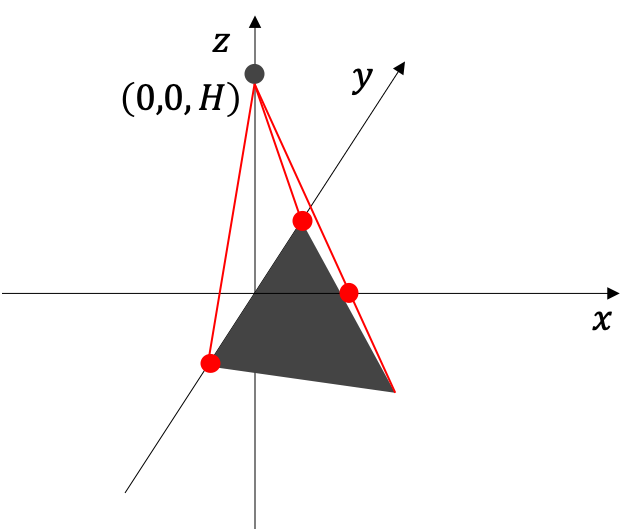
5. 4で求めた各点が正方形の3つの点を作るように各変数を決定する

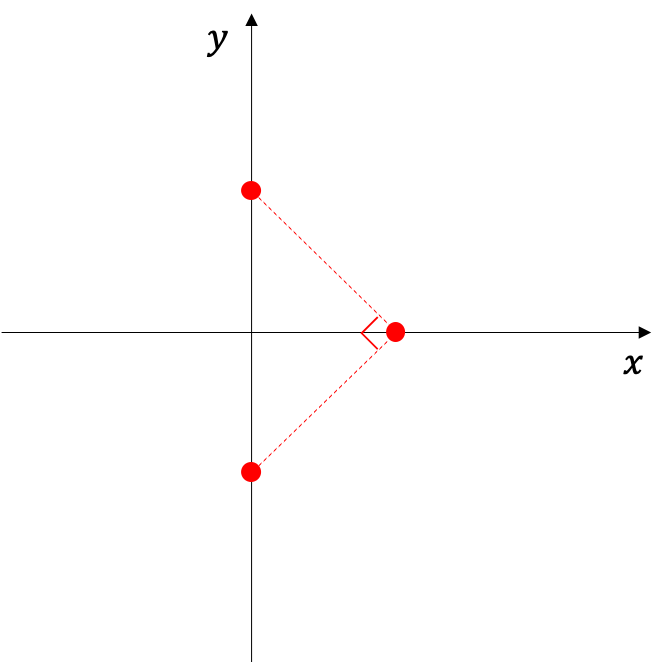
6. 同様に視線とxy平面との交点が正方形のもう１点に一致するように錐を作る

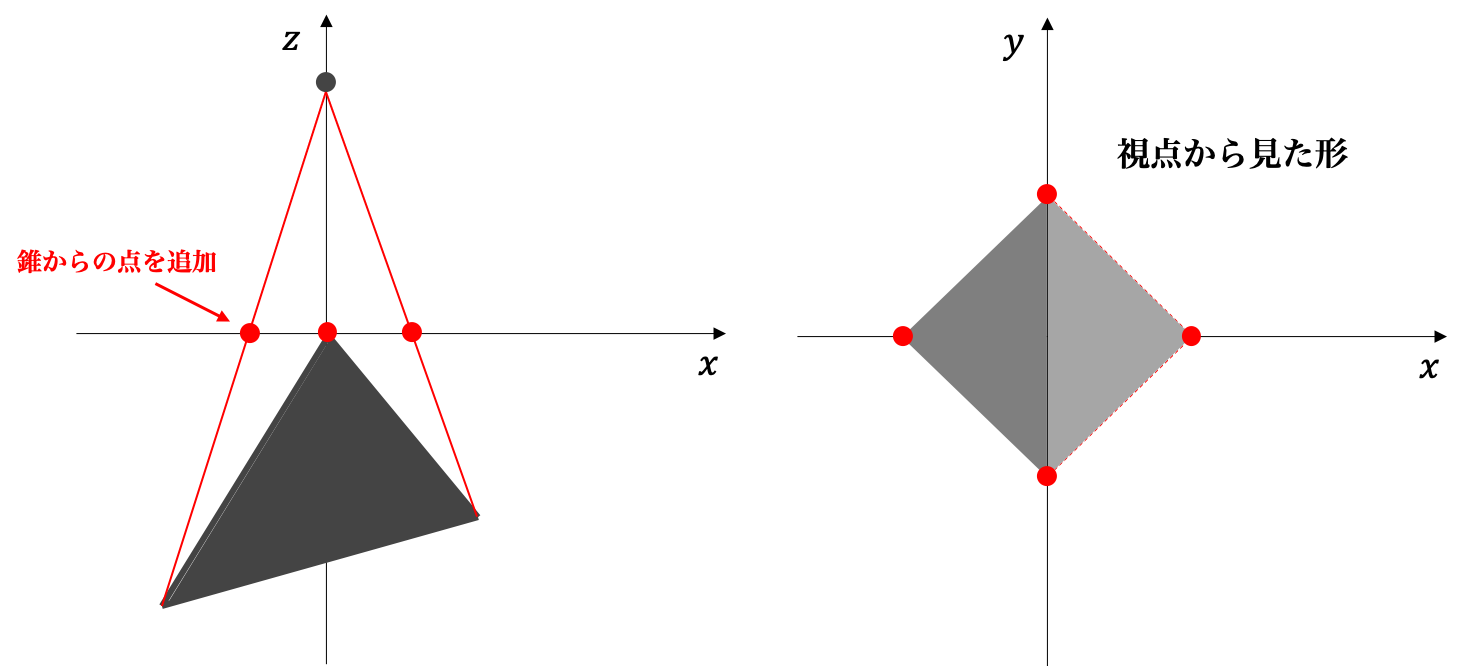
これで正三角形から正方形を作る方法が計算できるはずです。

次回、実際の計算と実験をしていきます。