前回

正方形を底面に持つ錐（ピラミッド型）を斜めにしたら五角形に見えることから、以下のような問題を考えました。

遠近法を考慮することで正四角錐から正五角形を作ることは可能か。

また、一般的に正n角錐から正n+1角形を作ることは可能か。可能とすればどのようにすれば良いか

これからこの問題について考えたことを話していきます。

遠近法の計算

まず最初に遠近法によって対象の見かけ上の大きさをどのように計算すれば良いのかを考えました。

最初の考え

まず私は以下のように考えました。

対象を見た時の見かけの大きさは視点と対象の距離に反比例する

つまりこういうことです。

例えば視点から5cmの距離に長さ10cmの棒があったとします。このときの見かけの大きさをAとします。

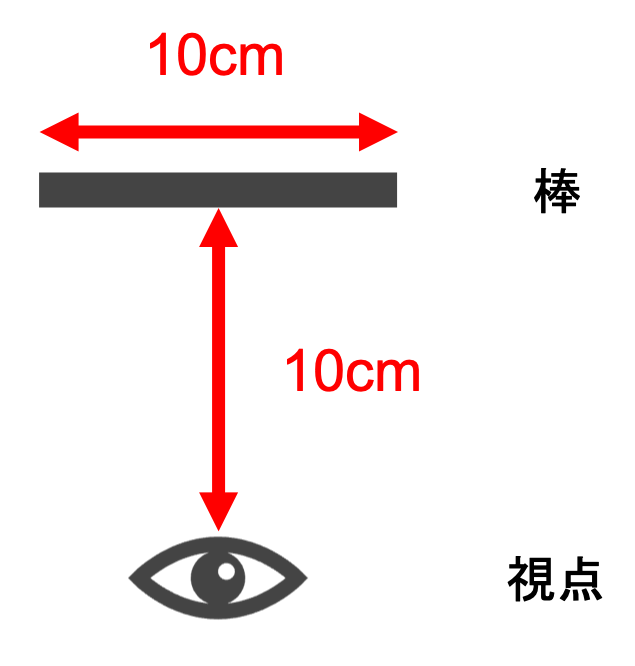
この棒を視点から20cmのところまで離したとします。このときの見かけの大きさをBとします。

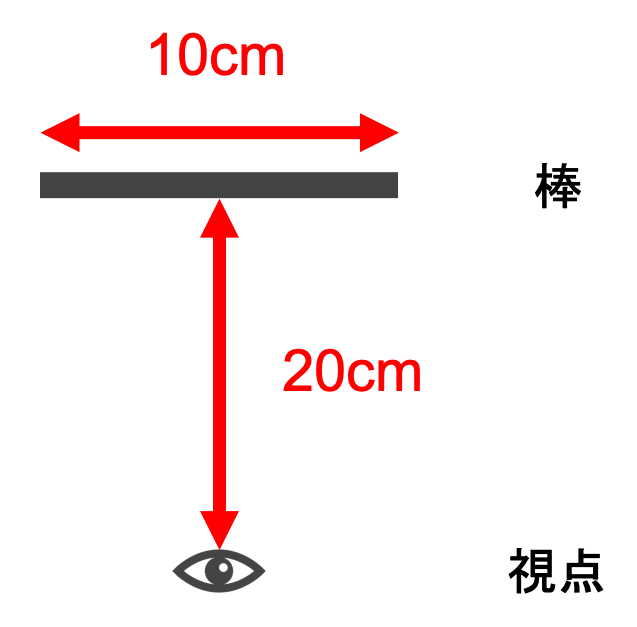
このとき、AとBの間で次の関係が成り立つ。

A = 2B

このように距離に反比例して見かけの長さが短くなるというのがこの考えです。

ということで、この考えから正方形から正五角形を作る方法を考えてみました。

正方形から正五角形を作る（失敗）

上の遠近法の計算方法を使って正方形から正五角形を作っていきます。

正五角形の特徴

まず正五角形についての確認です。

正五角形は以下のような特徴があります。

①１つ飛ばした点を結ぶ対角線が辺の長さの黄金比倍になる

②①の対角線で分けた２つの図形の高さの比はsin36°:cos18°

黄金比とは(1+√5)/2のことでφで表されます。

つまり以下の図のようになります。

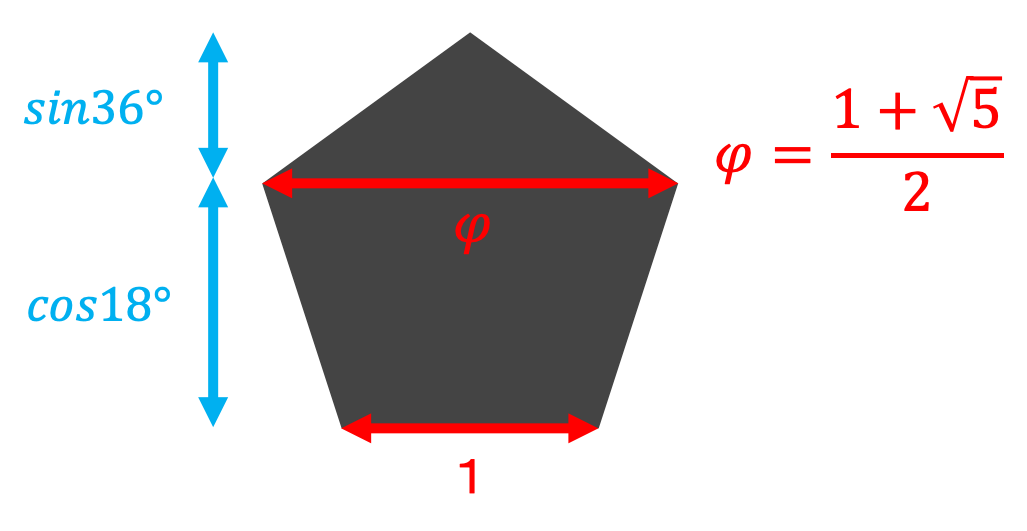
これを踏まえて上の遠近法で考えると以下のように計算できます。

1. 視点からの距離がxの位置に１辺がaの正方形を配置する
2. 手前の辺と奥の辺の距離の比が1:φになるように正方形をθ傾ける
3. 図のように高さの比率がsin36°:cos18°になるような条件を求める
4. 横幅と高さの比率も図のようになるように錐の頂点を決める

それでは計算していきましょう。

計算

⒈ 視点からの距離がxの位置に１辺がaの正方形を配置する

これは計算というより条件設定です。

以下の図のような条件設定になります。

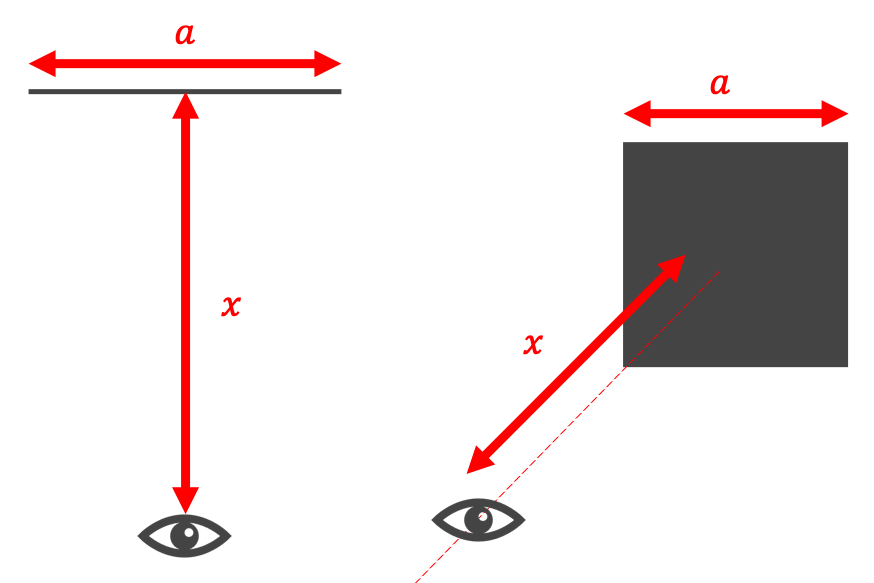
2. 手前の辺と奥の辺の距離の比が 1 : φ になるように正方形を θ 傾ける

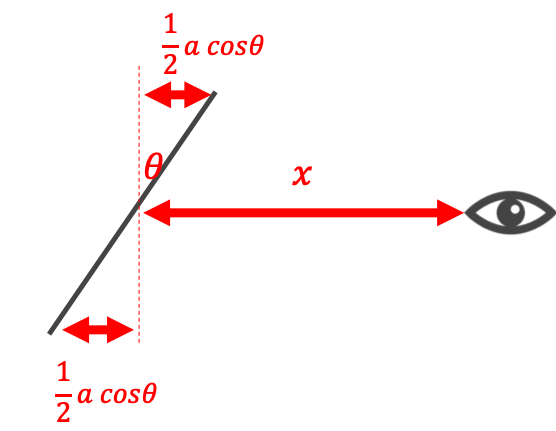
この計算は以下のようになります。

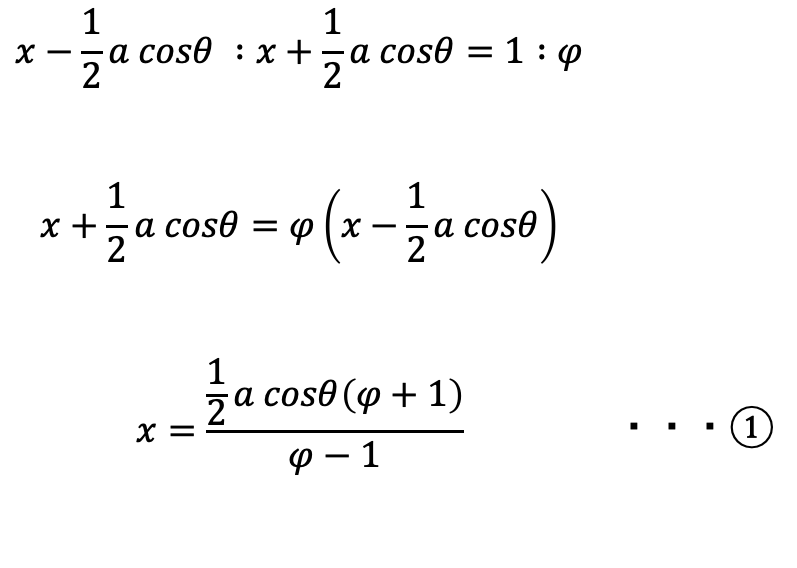
3. 正五角形の頂点に点が重なるように錐の高さを求める

さてここで縦方向にもうまく点を配置できればうまくいく、、、

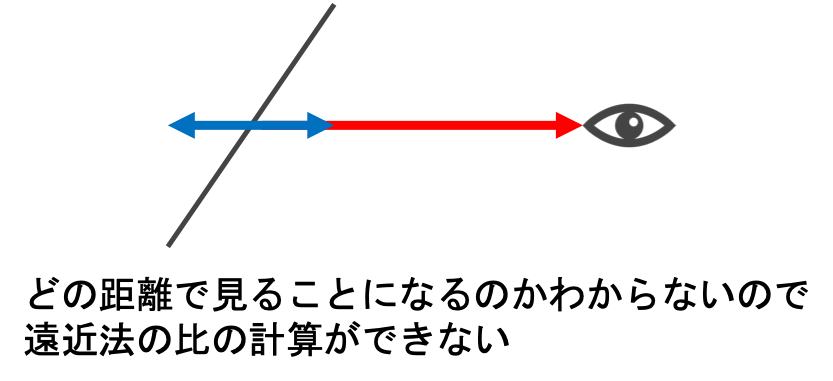
と思ったのですが、縦方向の長さがどのように見えるのか上の計算方法ではわかりませんでした。

そもそも上の遠近法の計算方法は対象のすべての点が同一距離にあるときに成立することだと気がつきました。

2の計算も厳密には三平方の定理を使って各辺の高さも考慮しなければならないことに気がつきました。

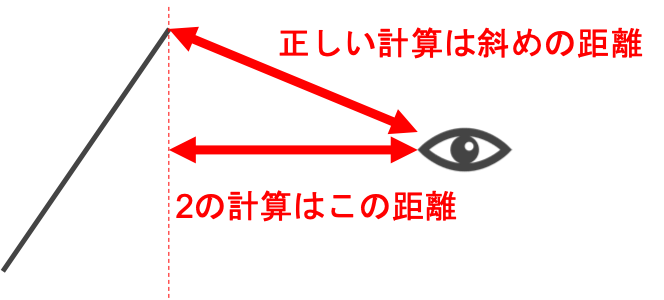
こうして、この方法では計算が複雑になったり、方法がわからなくなったりしてしまいました。

遠近法（視点から見てどのように見えるか）をもっと効率よく計算する方法はないでしょうか？

次回へ続きます。