きっかけ

ある日、数学のとある問題を考えていた。（この問題についてはまた別の回で記事にする！）

その問題を考えている過程で次のようなことに気づいた。

ピラミッドのような正四角錐を斜めにして見れば五角形に見える

つまりこういうことだ。

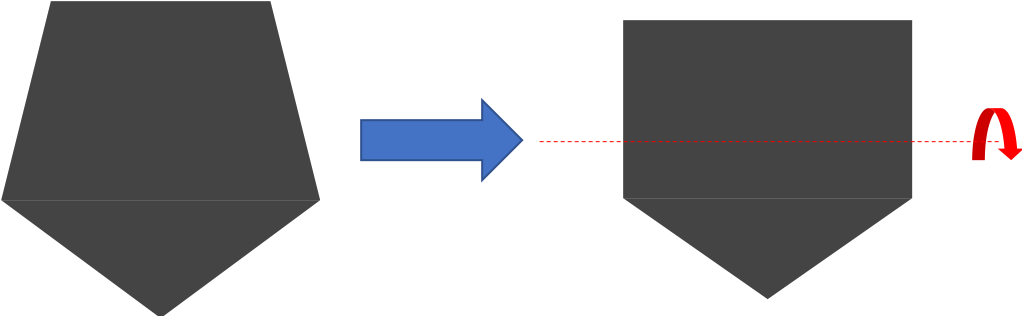
ここに正方形がある。

これを左右の軸を中心に回転させると

このように遠近法で手前の辺は長く、奥の辺は短く見える。

これがピラミッドのような錐であれば

このように五角形に見えるのではないかと考えた。

ここから少しだけ想像してみた。

正三角形から正四角形

正五角形から正六角形

・・・

想像ではなんとなく成り立つように感じた。

例えば5から6も頂点を下にして回転させれば短い辺が遠近法で長く見えいい感じになるかもと思った。

これが一般的に成り立ったら面白いなと思い研究を始めた。

問題

さて、

改めて、私が考えた問題をまとめると以下のようなものです。

遠近法を考慮することで正四角錐から正五角形を作ることは可能か。

また、一般的に正n角錐から正n+1角形を作ることは可能か。可能であるとすればどのようにすれば良いか

いきなり正四角錐から始まっているのは思いついたきっかけが正四角錐から正五角形だったからである。

一番小さいものは正三角錐（底面が正三角形の三角錐）から正方形を作ることだろう。

これは少なくとも正三角形を正方形の半分の直角二等辺三角形として見ることは可能だろう。

奥まで傾ければ角度が180°になり、傾けなければ60°だから必ず間に90°があるはずだ。

このあたりも踏まえて、考えたことを何回かに分けて記事にしていこうと思う。