前回

---

 

前回、底面が正三角形の錐を正方形として見る方法を考えた。

 

流れはおおまかに以下のようだった。

 

 

1. xy平面に正三角形を配置する

 

2. z軸上に視点を配置する

 

3. 三角形を回転させる

 

4. 三角形の各頂点と視点を結び、その線分とxy平面との交点を求める

 

5. 4の式が正方形の3点に合致するように方程式を立て、各パラメータを求める

 

6. 「xy平面上の正方形のもう１つの頂点と視点を通る直線」と「回転させた三角形の重心を通る垂線」との交点を求める

 

 

今回はこれに沿って実際に計算と実験をしていきたいと思います。

 

 

 

計算

---

 

xy平面に正三角形を配置する

 

１辺の長さがaの正三角形を上の画像のように配置する。

各点の座標も画像のように(√3/2a, 0, 0)、(0, 1/2a, 0)、(0, -1/2a, 0)となる

 

 

z軸上に視点を配置する

 

z軸上の高さHの点に視点を置く。

 

 

三角形を回転させる

 

 

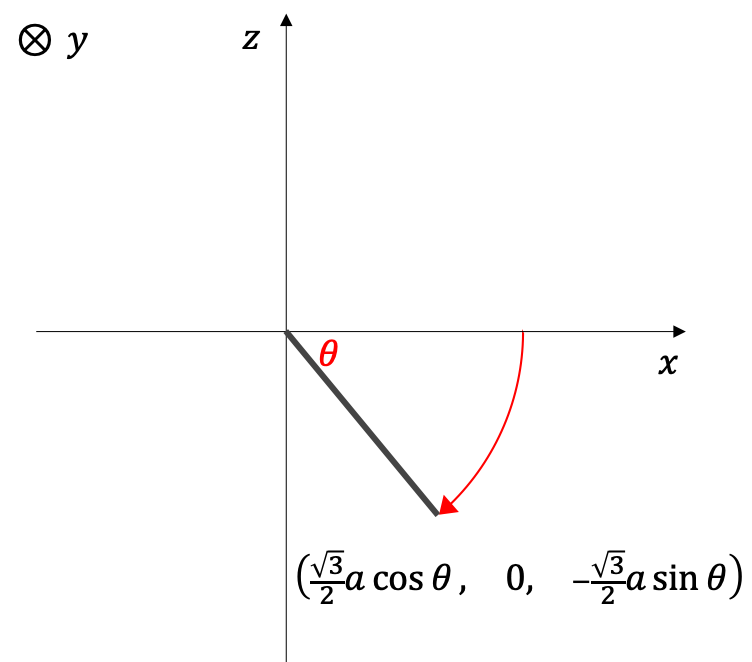
y軸を中心に三角形をθ 回転させる。

この時、三角形の(√3/2a, 0, 0)にあった頂点が(√3/2a cosθ, 0, -√3/2a sinθ)に移動する。

 

 

三角形の各頂点と視点を結び、その線分とxy平面との交点を求める

 

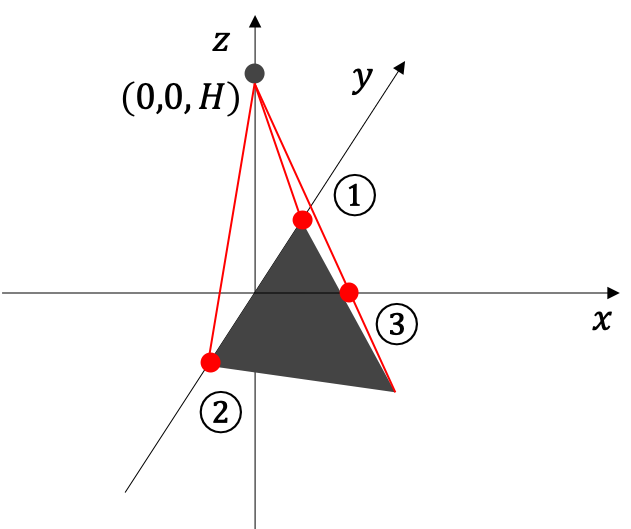①

 

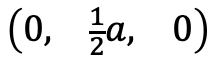
②

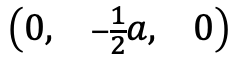
③簡単なベクトルの計算で以下のようになる

 

 

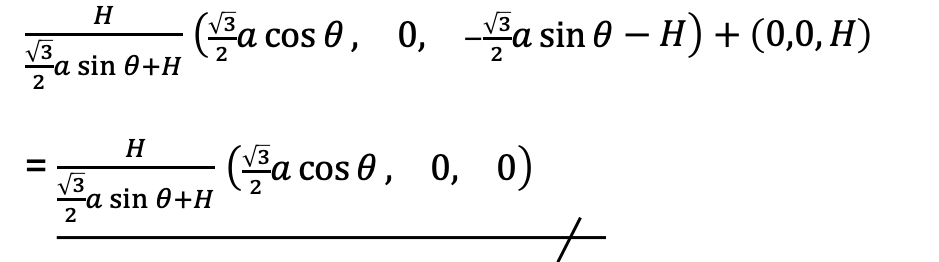
4の式が正方形の3点に合致するように方程式を立て、各パラメータを求める

 

①、②の点は固定なので③のみ計算すれば良い。

①②③の各点が正方形の３点に一致するには原点からの距離がすべて等しくなれば良いので以下のように計算する

この結果を改めて①とします。

 

 

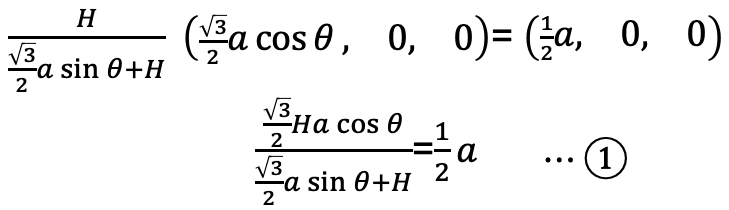
「xy平面上の正方形のもう１つの頂点と視点を通る直線」と「回転させた三角形の重心を通る垂線」との交点を求める

 

これについてはまず少し解説する。

 

この計算は三角錐の頂点を求めるもので、

 

xy平面上の正方形のもう１つの頂点と視点を通る直線とは視点から正方形の最後の点を通る直線である。（正方形の３点はすでに定まっているのでもう一点も定まっている）

 

回転させた三角形の重心を通る垂線とは錐の高さにあたる直線で、錐の頂点と底面を結んでいる直線である。

 

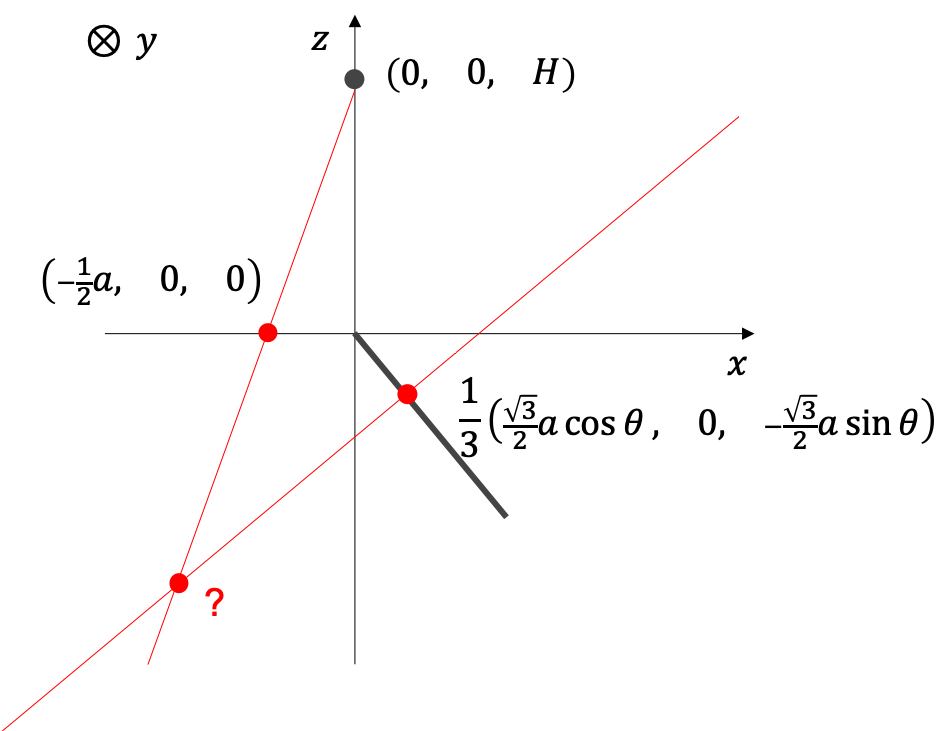
この計算は以下のようになる。

 

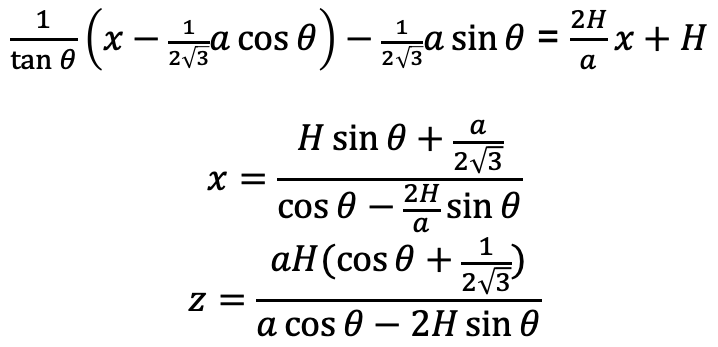
これにより三角錐のすべての点の座標がもとまった。

ここでa は定数で、求めるべきパラメータはθ とH の２つである。

 

２つのパラメータを定めるための方程式は①のみなので１つは任意となる。

 

 

 

実験 

---

 

ということで実験する。

実験しやすいようにθ を45°として実験してみる。（30°と60°もやりやすいが、計算してみればわかるようにこれらは実験できない）

 

θ=45°

θ が45°のときの各パラメータを計算すると以下のようになる。

 

 

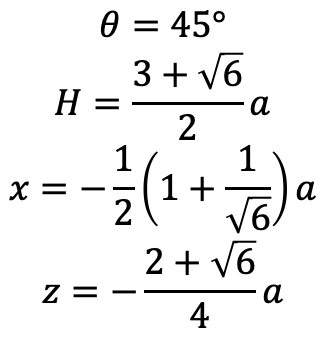
このパラメータどおりに錐の作成、視点の設定を行う。

 

以下の画像のように錐を作成した。

 

 

 

 

 

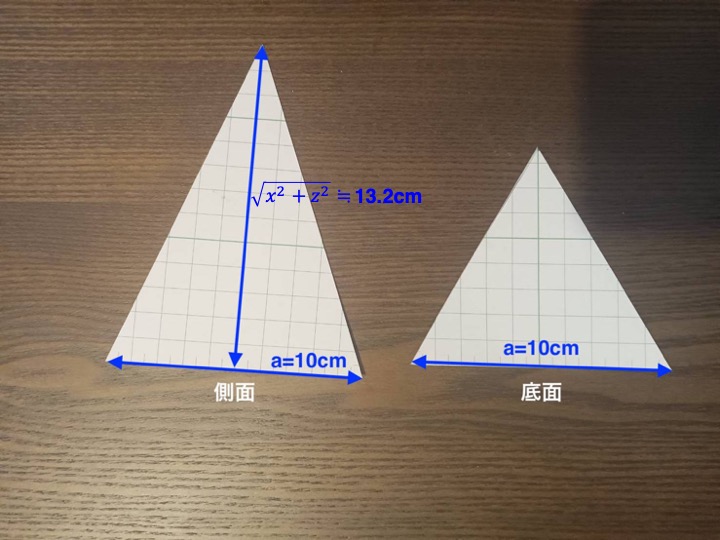
この錐とカメラ（視点）を以下のように設置する

 

 

この装置のカメラで写真を撮ればそこには正方形が写っているはずである。

 

 

結果

 

実際にカメラで写真を撮ってみた画像がこれだ。

 

 

 

本当に正方形になっている。

 

 

 

筆者はこの写真が撮れたときとても感動した。

 

今回のまとめ

---

 

今回は前回の考えをもとに計算し、実験してみた。

 

それにより実際に正三角形から錐をつくり正方形を作成することが可能であることがわかった。

今回の3→4は任意パラメータが残ったので装置のパターンはいくつもあると思う。

 

今度、正四面体を正方形としてみるパラメータを求めてみようと思う。何か面白い数になっているかもしれない。

 

次の回からは今回の計算方法を一般化し、n→n+1が可能かどうかを考えていく。

 

お楽しみに！