群とは

いきなりだが、群とはある集合とその集合上に定義された積の組（G,・）で以下を満たすものである。

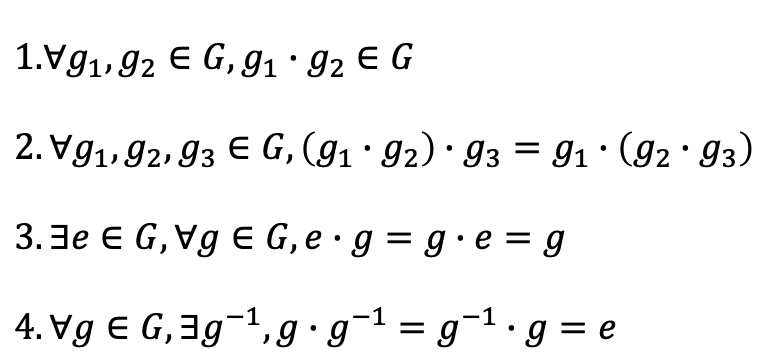
これを見ただけでその凄さや有用性がわかる方はいないだろう（いたら是非ともフィールズ賞とか目指してくれ）

これから何回かに分けてこの群の性質や応用について話していく。

ここでは導入的な話をしていこうと思う。

対称性について

数は大きさをはかるものである。

対して群は対称性をはかる。

これが群の特徴である。

対称性にはどのようなものがあるだろうか。

正三角形を例に見てみる。

各頂点に1,2,3と番号を振り、一回の操作してみる。

このように正三角形には6つの（一回で）対称的な図形に変換する操作がある。

これらの操作を組み合わせるとどうなるだろうか。

例えば、120°反時計回りに回転する操作と上下に通る直線を軸に反転させる操作を組み合わせてみる。

これも対称的な図形（元の正三角形と同じ図形）になった。

そして、これは「2軸回転」と同じである。

このように対称的な図形に変換する操作はそれらを組み合わせても同様の操作になる。

つまり、以下のような集合と積を考えると、その組（G, ・）は群の公理1を満たす。

また、公理2を考察すると以下のようになる。

以下の例で考えてみる。

g1：120°回転

g2：上下軸で反転

g3：240°回転

とすると、

(g1・g2)・g3は「240°回転したあとに、上下軸で反転して120°回転する操作をする」ことになる。

g1・(g2・g3)は「240°回転して上下軸で反転したあとに、120°回転する操作をする」ことになる。

文章が変わっただけで操作は変わっていない。（最近のAIはこれを認識できるだろうか）

公理3,4はわかりやすいだろう。

回転なら逆回転、反転なら再反転すると元に戻る。組み合わせの逆元も作れる。

単位元は「何もしない」操作である。

このように「対称図形に変換する操作」は群をなす。

また、各操作に各対称図形が対応していることがわかる。

つまり図形の対称性がわかるのだ。

「対称性をはかる」の意味が少しわかったと思う。

歴史

話は変わって、群論の歴史の話をする。

そもそも群論はどのような経緯で誕生したのだろうか。

群の概念が生まれたのは、当時まだ10代のエヴァリスト・ガロアによる代数方程式の研究が発端だと言われている。

ガロアは代数方程式の解がもつ対称性に着目し、それを群として扱うことで「5次以上の方程式には代数的な解の公式が存在しない」ことを証明した。

これがきっかけで群という概念が研究され、これまで発展してきた。

今では最先端の物理学でも欠かせない概念となっている。

ちなみに、ガロアは悲運の数学者などとよく言われる。

数学の才を発揮していたが、なかなか認められず（あるいは運悪く）政治的なことに巻き込まれ決闘で亡くなったのである。

（そのあたりのことについては陰謀説がある）

決闘の直前に友人に宛てた手紙に「僕にはもう時間がない」と記して数学の多くの発見を残したことは有名な話だ。

彼が認められ、長く生きていたら数学はもっと発展していたかもしれない。

次回から

次回からは本格的に群論の解説に入っていく。

まずは、群の公理から入っていこうと思う。